persamaan lingkaran

Rumus Persamaan Lingkaran Matematika

Rumus Web mengumpulkan materi Rumus Persamaan Lingkaran Matematika ini untuk anak SMA demi UAN SNMPTN SPMB SIMAK UI. Silakan dipelajari

A. Persamaan Lingkaran yang berpusat di O (0, 0) dan berjari-jari r.

Dari gambar, diperoleh persamaan : OP = r

Sehingga diperoleh persamaan lingkaran dengan pusat di O dan berjari-jari r , yaitu :

Suatu titik A dikatakan :
a. Terletak pada lingkaran
b. Terletak di dalam lingkaran
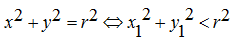
c. Terletak di luar lingkaran
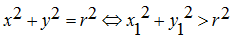
B. Persamaan Lingkaran yang berpusat di P (a, b) dan berjari-jari r.

Gambar di atas adalah sebuah lingkaran dengan pusat (a, b) dan berjari-jari r. Titik Q (x, y) adalah sebuah titik pada lingkaran.
Dari gambar diperoleh persamaan : PQ = r

Sehingga diperoleh persamaan lingkaran dengan pusat di P (a, b) dan berjari-jari r, yaitu :
Suatu titik A dikatakan :
a. Terletak pada lingkaran
b. Terletak di dalam lingkaran
c. Terletak di luar lingkaran
C. Persamaan Umum Lingkaran
Bila kita menjabarkan persamaan :

Dan mengatur kembali suku-sukunya, maka akan diperoleh :

Persamaan terakhir dapat pula dinyatakan dengan :

Dengan :


Persamaan (3) merupakan persamaan lingkaran dengan pusat di dan berjari-jari



sumber : http://www.rumus.web.id/matematika/rumus-persamaan-lingkaran-matematika/